norm 函数

scipy.stats.norm 函数 正态分布

scipy.stats.norm函数可以实现正态分布（也就是高斯分布）

norm(loc=,scale=) # loc: mean 均值， scale: standard deviation 标准差

生成服从指定分布的随机数

norm.rvs() 通过 loc和scale 参数可以指定随机变量的偏移和缩放参数，这里对应的是正态分布的期望和标准差。size 得到随机数数组的形状参数。(也可以使用np.random.normal(loc=0.0, scale=1.0, size=None))

求概率密度函数指定点的函数值

stats.norm.pdf 正态分布概率密度函数。

标准形式是：

$f(x)=\frac{\exp \left(-x^{2} / 2\right)}{\sqrt{2 \pi}}$

import matplotlib.pyplot as plt
import seaborn as sns

from scipy.stats import norm
import numpy as np
sns.set_style('whitegrid')

np.random.seed(1)
X = np.linspace(-5,5,20)

# 第一种调用方式
gauss = norm(loc=1,scale=2) # loc: mean 均值， scale: standard deviation 标准差
r_1 = gauss.pdf(X)

# 第二种调用方式
r_2 = norm.pdf(X, loc=0, scale=2)

for i in range(len(X)):
    plt.scatter(X[i], 0, s=50)
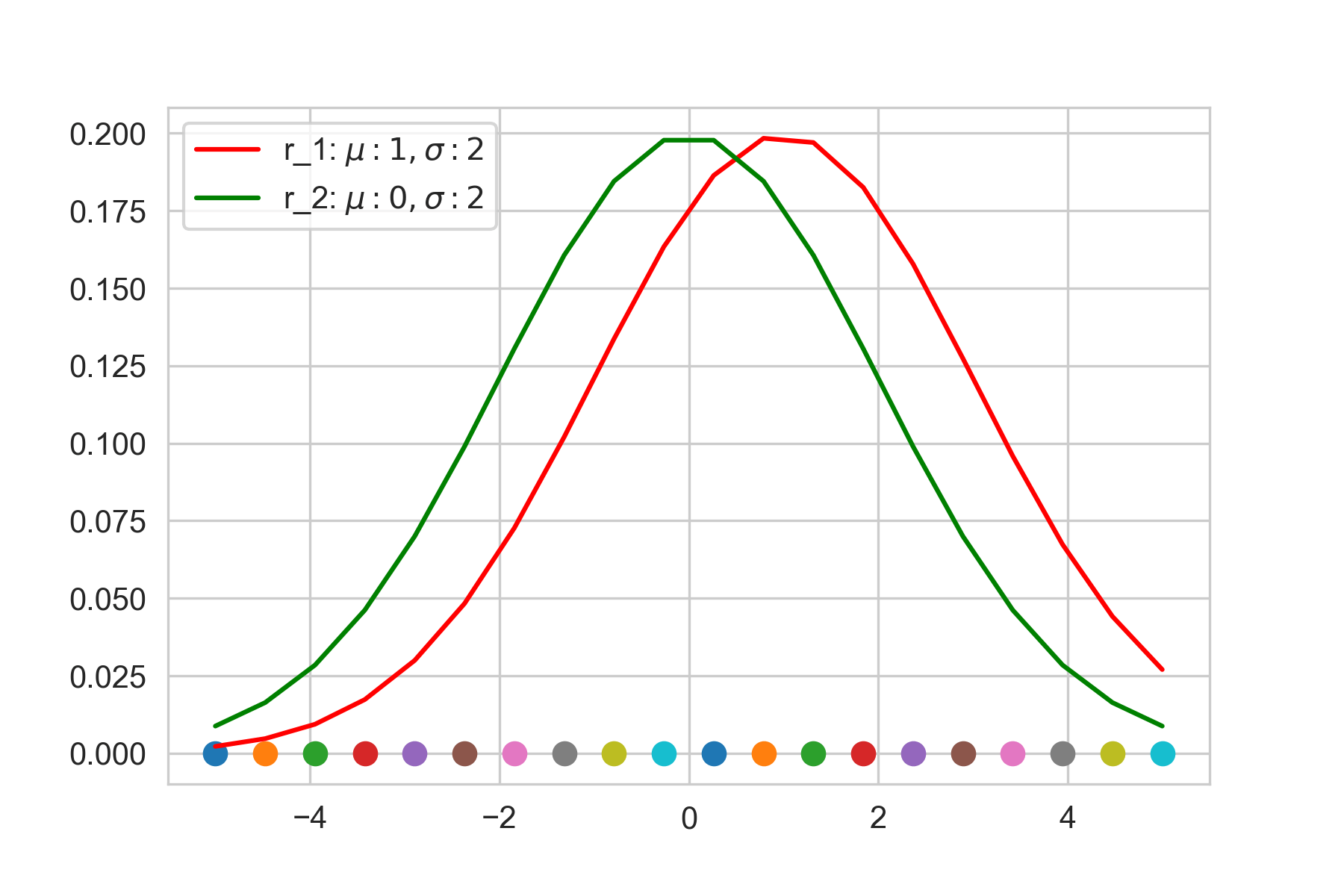
for g, c ,l in zip([r_1, r_2], ['r', 'g'],['r_1: $\mu:1,\sigma:2$','r_2: $\mu:0,\sigma:2$']):  # 'r': red, 'g':green
    plt.plot(X, g, c=c,label=l)

plt.legend()
plt.show()

标准正态分布表与常用值

• Z-score 是非标准正态分布标准化后的 x即 ：$z=\frac{x-\mu}{\sigma}$

• 表头的横向表示小数点后第二位，表头的纵向则为整数部分以及小数点后第一位；两者联合作为完整的 x，坐标轴的横轴

• 表中的值为图中红色区域的面积，也即 cdf，连续分布的累积概率函数，记为 $\Phi(x)$

• cdf 的逆，记为$\Phi^{-1}(x)$ ，如$\Phi^{-1}(3/4)$ ，表示 x 取何值时，阴影部分的面积为 0.75，查表可知，x 介于 0.67 和 0.68 之间；

  from scipy.stats import norm
  norm.ppf(3/4)
  # 0.6744897501960817
  

cdf 与 ppf（分位函数）

from scipy.stats import norm

覆盖的概率范围：

norm.cdf(1) - norm.cdf(-1)
# 0.6826894921370859

norm.cdf(2) - norm.cdf(-2)
# 0.9544997361036416

norm.cdf(3) - norm.cdf(-3)
# 0.9973002039367398

求累计分布函数指定点的函数值

stats.norm.cdf正态分布累计概率密度函数。

$\Phi(x)$ 为 累积概率密度函数，也即 cdf：

norm.cdf(0)
# 0.5

累计分布函数的逆函数

stats.norm.ppf正态分布的累计分布函数的逆函数，即下分位点。

$\Phi^{-1}(x)$ 通过 ppf(x)进行计算：

>> from scipy.stats import norm
# Q3 分位点；
>> norm.ppf(3/4)
# 0.6744897501960817
# 即 Q3 分位点处的横坐标取值为 0.6744897501960817



# Q1 分位点
>> norm.ppf(1/4)
-0.6744897501960817

例如 在某一假设检验中，计算得到的 $z=3.125$

# 当 α=0.01 时 ,通过查表的 z_{0.01}=2.33 ,此时的 z_{0.01} 可以通过 `norm.ppf` 计算的到
from scipy.stats import norm
norm.ppf(1-0.01)
# 2.3263478740408408

参考

• 标准正态分布表（scipy.stats）
• scipy.stats.norm函数
• python统计函数库scipy.stats的用法解析